A variational approach to non-rigid image registration with Bregman divergences and multiple features
Abstract
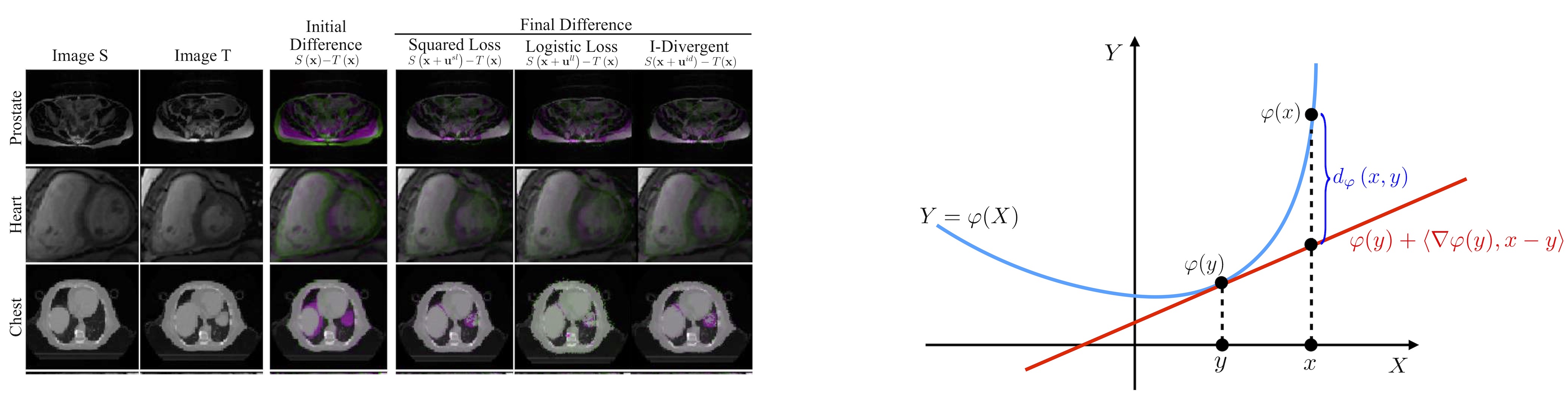
Variational methods register images by minimizing functionals that balance measures of smoothness and image similarity. However, the specificity of image-similarity measures can limit the application of variational methods. To address this issue, we propose a new energy functional that generalizes the classical variational method for nonrigid image registration. Our generalization uses Bregman divergences as the similarity measure of the registration functional. These divergences include a number of important similarity measures, such as the Squared Loss distance, the KL divergence, the Logistic Loss, the Mahalanobis distance, the Itakura-Saito divergence, and the I-divergence. We derive the Euler Lagrange and gradient-flow equations associated with the new functional. By using Bregman divergences, our registration method can combine various types of image characterization as well as spatial and statistical information. Our experiments show that the use of Bregman divergences improves registration quality.